Al nosotros derivar por primera vez una función que este en función de X y Y, su derivada también será una función que dependa de las variables independientes X y Y. Es por esta razón que nosotros podemos volver a derivar esta función ya sea con respecto a X o a Y. A estas derivadas se les conoce como las derivadas de orden superior y su orden esta dado por el número de veces que hemos derivado a la función inicial. Ejemplo:
INCREMENTOS Y DIFERENCIALES.
El incremento total que sufre una función se puede expresar de la siguiente manera:
.png.jpg)
Hay que tener muy en cuenta que el incremento total de la función no es igual a la suma de los incrementos parciales con respecto a X o Y.
Sin embargo cuando se trabaja con incrementos que son muy pequeños tanto así que se los lleve al límite cuando estos ya tiendan a cero, el incremento de Z se convierte en un diferencial de Z y en este caso el diferencial de Z es aproximadamente igual a la suma de las derivadas parciales de Z con respecto a X e Y, multiplicadas por su respectivo diferencial de X o Y.
.png.jpg)
Hay que señalar que cuando se calcula diferenciales se esta calculando un valor aproximado del valor real del incremento.
DERIVACIÓN DE FUNCIONES COMPUESTAS.
Suponemos la función Z=f(x,y), y que tanto x como y dependan de una tercera variable llamada t, entonces aplicando la regla de la cadena la derivada de Z con respecto a t sería:
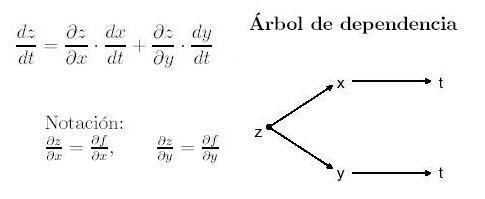
Hay que recalcar que la derivada/s que interesa hallar es con respecto a la variable/s independiente/s.
Si se desea hallar derivadas de orden superior en estos casos hay que tomar muy en cuenta la regla de la cadena en cada caso y la propiedad de la derivada cuando se deriva un producto de dos funciones.
DIFERENCIALES DE ORDEN SUPERIOR
En este caso se muestra la diferencial de orden 2 de una función de dos variables, hay que tomar en cuenta de que si la función depende de más variables o a su vez si se desea sacar un diferencial de orden mayor los términos cambiaran y al igual que en el caso de las derivadas de orden superior para funciones compuestas es necesario tomar en cuenta las propiedades de la diferenciación del producto de dos funciones.
DERIVACIÓN DE FUNCIONES IMPLÍCITAS.
Es muy importante que primero antes de realizar cualquier operación se identifiquen claramente cuales son las variables independientes ya que las derivadas que interesan serán con respecto a estas variables. Existen dos métodos para hallar estas derivadas pero en sí los dos métodos conducen a la mismas ecuaciones.
1. Por diferenciación:

 se llegan a tener estas dos derivadas que son las que tenemos que remplazar en la diferencial principal para poder hallar la derivada de z con respecto a una de estas dos variables, ya que X depende de Y, y Y depende de X.
se llegan a tener estas dos derivadas que son las que tenemos que remplazar en la diferencial principal para poder hallar la derivada de z con respecto a una de estas dos variables, ya que X depende de Y, y Y depende de X.
1. Por derivación implícita:
Al igual que en el método de arriba el resultado final es:

 que se deberá remplazar en las derivada de z con respecto a una de estas dos variables tal como en el caso anterior.
que se deberá remplazar en las derivada de z con respecto a una de estas dos variables tal como en el caso anterior.
SISTEMA DE FUNCIONES IMPLÍCITAS.
Al igual que en el caso de la derivada de funciones implícitas, el objetivo principal aquí es encontrar las derivada de una o más de las funciones puestas con respecto a las variables independientes.
Estos problemas se pueden resolver por medio de los siguientes métodos:
.png.jpg)
1. Por diferenciación:
.png.jpg)
como en este caso las variables independientes son u y v, se desea despejar dx y dy en el sistema de ecuaiones y dejarlas en función de du y dv para así poder remplazar en el diferencial de Z y obtener las correspondientes derivadas.
2. Por derivación implícita:
Primero se debe derivar las funciones con respecto a cada una de las variables que existen
.png.jpg)
pero hay que tener en cuenta que las u y v son independientes por lo que la derivada de estas con respecto a sí mismo son 1 y las otras son cero, simplificándose así el sistema de funciones y resultando en uno donde las derivadas de las variables intermedias con respecto a las independientes pueden ser despejadas y encontradas, para luego ser remplazadas en la derivada de Z con respecto a las variables independientes.
3. Por Jacobianos:
En este método primero hallamos el jacobiano D que es igual a:
.png.jpg)
una ves hallado D, se utiliza las relaciones de que la derivada parcial de Z con respecto a U es igual a -D1/D, donde D1 es el un determinante jacobiano parecido a D pero que en lugar de ir Z ponemos la variable independiente U.
.png.jpg)
Repetimos el paso anterior para la otra variable independiente.
DERIVADAS DIRECCIONALES.
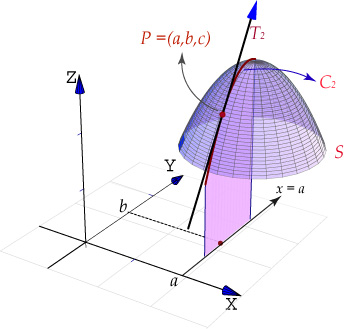
Estas variables representan la tasa de variación de la función f, en la dirección de un vector dado. Esta derivada se la calcula por:

donde:
 es el vector gradiente de la función f.
es el vector gradiente de la función f.
No hay comentarios:
Publicar un comentario