NOVIEMBRE

FUNCIONES DE DOS O MAS VARIABLES

Donde X1, X2, X3, ..., Xn: don variables independientes y Z: vaeriable dependiente.

Si n=2; Serán funciones de dos variables cuyo dominio y rango son los siguientes:

La gráfica de la función f de dos variables es el conjunto de todos puntos (x, y, f(x, y)) en espacio tridimensional, donde restringimos los valores de (x, y) a estar en el dominio de f. En otras palabras, la gráfica es el conjunto de todos puntos (x, y, z) tal que z = f(x, y).

La gráfica de una función de tres variables es imposible de realizar, a esta gráfica se la llama HIPERSUPERFICIE y lo único que podríamos graficar sería su dominio que es una superficie en el espacio.

ANÁLISIS DEL DOMINIO DE DEFINICIÓN O CAMPO DE EXISTENCIA.

Este análisis consta de tres pasos:

1. Análisis Matemático - Parte Analítica.

2. Análisis Gráfico - Parte Gráfica.

3. Análisis Descriptivo - Parte Descriptiva.

Para que quede mas claro realicemos el siguiente ejemplo:

III. Análisis Descriptivo - Parte Descriptiva: El dominio de la función son todos los pares ordenados (x,y) tal que esten ubicados por sobre la recta y=-1-x y con x diferente de 1.

CURVAS DE NIVEL.

Las curvas de nivel de una función son las curvas cuyas ecuaciones son f(x,y)=k; donde k es una constante que está dentro del rango de la función.

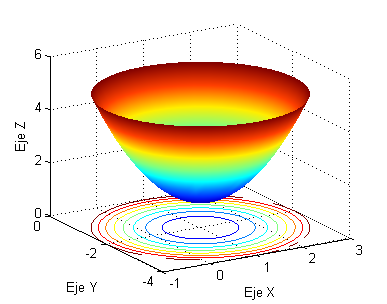
Para poder graficarlas deberemos remplazar z por una constante k, haciendo así que la superficie se interseque con planos paralelos al plano XOY y poder sacar las correspondientes curvas de nivel.

Si f(x,y,z)=k, entonces se generaran las SUPERFICIES DE NIVEL.

Si f(x,y,z,w)=k, entonces se generaran las HIPERSUPERFICIES DE NIVEL.

LIMITES Y CONTINUIDAD.

El límite de las funciones de dos variables está definido por:

Como podemos observar el entorno de aproximación es un disco de centro (a,b) o (Xo,Yo); y de radio delta.

Para determinar el límite de una función de dos variables (estos métodos también se aplican para funciones de n variables) se tienen infinitos caminos de aproximación, por lo tanto:

• Si por dos o más caminos o trayectorias, el valor del límite es diferente, entonces se concluye que el límite no existe.
• Si por dos o más caminos el valor del límite es el mismo, suponemos que el límite existe y debemos proceder a demostrar su existencia ya sea por la definición, aplicando el teorema del sánduche, o mediante el uso de coordenadas polares.

Ejemplos:

Dado que no todas las pruebas dan el mismo resultado podemos concluir que el limite no existe.

2. Ver el siguiente video: EJEMPLO 2 LIMITES

CONTINUIDAD

Sean f(x,y)=z una función de dos variables, se dice que es continua en (Xo, Yo) si cumple:

Si una función no cumple este requisito se dice que es discontinua y abra que evaluar que discontinuidad presenta la función:

• No existe f(Xo,Yo) pero si existe si límite, en este caso es discontinua evitable.
• Existe el limite de f cuando tiende a (Xo,Yo) pero es diferente de f(Xo,Yo), en este caso también es discontinua evitable.
• No exite el límite de la función cuando tiende a (Xo,Yo), en este caso se dice que es discontinua inevitable.

En el caso de que la función sea discontinua evitable se debe re definir, para transformarla en continua en (Xo,Yo).

DERIVADAS PARCIALES

La derivada parcial de f respecto a x es su derivada respecto a x, cuando los demás variables se consideran constantes.

En forma parecida, la derivada parcial de f respecto a y es su derivada respecto a y, cuando los demás variables se consideran constantes, y así sucesivamente para otras variables que pueda haber. Las derivadas parciales se escriben como ∂f/∂x, ∂f/∂y, y así sucesivamente. Se usa el símbolo "∂" (en lugar de "d") para recordarnos que hay mas que una variable, y que estamos considerando constantes las demás variables.

Las reglas y propiedades de derivación de funciones de una sola variable se aplican para las funciones de 2 o más variables.

Existe el mismo número de derivadas parciales que de variables independientes.

INTERPRETACIÓN FÍSICA

Las derivadas parciales físicamente se representan como una RAZÓN DE CAMBIO, cuanto varía f si "x" varía, manteniendo fija "y" o cuanto varía f si "y" varía, manteniendo fija "x".

INTERPRETACIÓN GEOMÉTRICA

Si f está una función de x y y, el proceso de tomar la derivada parcial ∂f/∂x y evaluarla a (a, b) es nada más que tomar constante y a y = b y calcular la razón de cambio de f en el punto x = a. Entonces, la derivada parcial es el pendiente de la recta tangente en el punto donde x = a y y = b, a lo largo del plano que pasa por y = b. (Vea la figura más abajo.)

De aquí se puede deducir que la ecuación del plano tangente a f(x,y) en un punto de coordenadas (Xo,Yo,Zo) es:

Dx(X-Xo) +Dy(Y-Yo)-1(Z-Zo)=0