MÁXIMOS Y MÍNIMOS RELATIVOS.
- Una función tiene un máximo relativo en (a,b), si f(x,y) es menor o igual a f(a,b) cuando (x,y) está cerca de (a,b).
-Una función tiene un mínimo relativo en (a,b), si f(x,y) es mayor o igual a f(a,b) cuando (x,y) está cerca de (a,b).

CRITERIO DE LA SEGUNDA DERIVADA.
1. Hallar las derivada parciales fx, fy.
2. Igualar a cero las derivadas parciales para hallar los puntos críticos.
3. Hallar las derivadas parciales de segundo orden: fxx, fxy, fyy.
4. Evaluar: A*C-B*B (determinante jessiano)
A=fxx|(xo,yo) B=fxy|(xo,yo) C=fyy|(xo,yo)
- Si el jessiano es mayor a 0; y A o C son menores a cero entonces hay un máximo relativo.
- Si el jessiano es mayor a 0; y A o C son mayores a cero entonces hay un mínimo relativo.
- Si el jessiano es menor a 0; hay un punto de silla.
- Si el jessiano es igual a cero, la existencia es indeterminada.
MÁXIMOS Y MÍNIMOS ABSOLUTOS.
Para poder evaluar estos puntos es necesario que la función este acotada y cerrada ya que es ahí en donde alcanza un valor máximo o mínimo, ya sea en un punto estacionario o en la frontera de la región.
Para calcularlos:
- Primero se evalúa en los puntos estacionarios, que son en los puntos críticos.
- Segundo se evalúa en los puntos de la frontera.
- Tercero se evalúa en los vértices en caso de haberlos.
- Por último se compara los valores de f en cada uno de estos puntos y se concluye cuales son máximos o mínimos.
MÉTODO DE MULTIPLICADORES DE LAGRANGE.
Este método sirve para cuando hay una restricción con las cuales las variables independientes estén relacionadas. A este se le llama extremo condicionado y puede ser máximo o mínimo.
La función de Lagrange es:
donde g(x,y) es la restricción que deben cumplir x e y. Si hay más de una restricción se deberán añadir mas multiplicadores lamda.
Luego se procede a derivar parcialmente la función de Lagrange con respecto a cada variable y lamda e igual a cero para formar un sistema de ecuaciones.
INTEGRALES MÚLTIPLES.

La integral múltiple de una función de dos variables representa el volumen del sólido contenido debajo de la curva f(x,y).
Para resolver estas integrales se debe integrar normalmente con respecto a la diferencial que se este evaluando, pero hay que tener muy presente la evaluación en los límites de integración para cada variable.
Si la integral es sobre una región rectangular, las integrales se llaman iteradas ya que no importa el orden de integración el resultado seguirá siendo el mismo.
.png.jpg)
INTEGRALES SOBRE REGIONES MÁS GENERALES:
En los casos más generales las integrales no se dan sobre regiones rectangulares, aquí los límites de integración de una variable serán una función, que deberá ser evaluada primero, y con respecto a la otra variable los límites de integración seran constantes, en este caso esta integral se desarrolla al último.
TRANSFORMACIÓN DE INTEGRALES MÚLTIPLES.
Muchas veces es necesario cambiar la región sobre la cual se integra a una región de forma rectangular, para esto se usa la siguiente relación:
.png.jpg)
- A coordenadas polares:
- A coordenadas cilíndricas:
- A coordenadas esféricas:

CENTROS DE MASA.
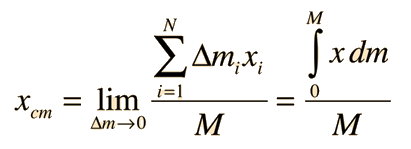
Con la fórmula de arriba se puede calcular el centro de masa con respecto al eje X, si se desean los centros de masa con respecto a los otros dos ejes solo se debe sustituir la Y o Z en lugar de la X.
Por lo general dm está en función de una función de densidad ya sea esta superficial, lineal o volumétrica, esta función de densidad puede ser constante cuando el cuerpo es uniforme o variable en este caso esta función de densidad dependerá de los valores X,Y,Z y entraran en la integral para ser resuelta.
MOMENTOS DE INERCIA.

Son los momentos de inercia con respecto a los ejes X, Y y al centro del sistema de referencia.
CAMPOS VECTORIALES.

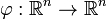 .
.
INTEGRALES DE LÍNEA.


Integral cuya función se encuentra evaluada sobre una curva C, la cual puede estar sobre un plano, o en el espacio. Para hallar esta integral se debe parametrizar tanto la curva como la función que se desea integrar.
![\int_C f\ ds = \int_a^b f(\mathbf{r}(t)) \|\mathbf{r}'(t)\|\, dt = \int_a^b f(\mathbf{x}(t),\mathbf{y}(t))\sqrt{[\mathbf{x}'(t)]^2+[\mathbf{y}'(t)]^2 }dt](http://upload.wikimedia.org/math/e/4/e/e4e3ce10c0f73e2212b1e717a10d9037.png)
INTEGRAL DE LÍNEA SOBRE CAMPOS VECTORIALES.

TEOREMA FUNDAMENTAL DE LAS INTEGRALES DE LINEA.
Si una función vectorial F, es conservativa entonces se cumple que:
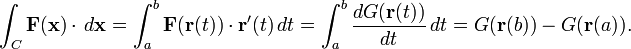
Donde G, es una función de potencial asociada a la función vectorial F.
Para comprobar si una función vectorial es de tipo conservativa, se usa el criterio de las derivadas cruzadas, si estas son iguales entonces se concluye que la fuerza es conservativa. Otro método es por medio del rotacional en donde si el rotacional nos da cero, entonces F es conservativa.
RELACIÓN ENTRE LAS INTEGRALES DE LÍNEA DE CAMPOS VECTORIALES CON CAMPOS ESCALARES.
.png.jpg)
Hay que recordar que la tano P,Q,R ya han sido parametrizadas en función de t antes por lo que restaría integrar en función del diferencial de t.
TEOREMA DE GREEN.
Este teorema nos permite transformar una integral de línea en una integral doble; esto permite encontrar la integral de línea sobre una curva cerrada, como si fuera el área encerrada por dicha curva.
ROTACIONAL.
Muestra la tendencia de un campo vectorial a inducir rotación alrededor de un punto. Se calcula por:

DIVERGENCIA.
La divergencia de un campo vectorial mide la diferencia entre el flujo saliente y el flujo entrante de un campo vectorial sobre la superficie que rodea a un volumen de control, por tanto, si el campo tiene "fuentes" la divergencia será positiva, y si tiene "sumideros", la divergencia será negativa.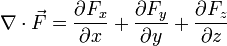
RELACIÓN ENTRE LAS INTEGRALES DE LÍNEA DE CAMPOS VECTORIALES CON CAMPOS ESCALARES.
.png.jpg)
Hay que recordar que la tano P,Q,R ya han sido parametrizadas en función de t antes por lo que restaría integrar en función del diferencial de t.
TEOREMA DE GREEN.
Este teorema nos permite transformar una integral de línea en una integral doble; esto permite encontrar la integral de línea sobre una curva cerrada, como si fuera el área encerrada por dicha curva.
ROTACIONAL.
Muestra la tendencia de un campo vectorial a inducir rotación alrededor de un punto. Se calcula por:

DIVERGENCIA.
La divergencia de un campo vectorial mide la diferencia entre el flujo saliente y el flujo entrante de un campo vectorial sobre la superficie que rodea a un volumen de control, por tanto, si el campo tiene "fuentes" la divergencia será positiva, y si tiene "sumideros", la divergencia será negativa.
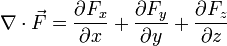
No hay comentarios:
Publicar un comentario