Cálculo Vectorial ;): OCTUBRE

Primera Clase.

En esta clase se comenzó dando una pequeña introducción a la geometría del espacio. En R2 una f(x,y)=0 representa una función implícita de dos variables y su gráfica representa una curva en el plano, la intersección de estas curvas generan puntos. En R3 f(x,y,z)=0 representa una función implícita de tres variables que geométricamente representa una superficie en el espacio, la intersección de dos superficies genera curvas, mientras que la intersección de tres superficies solo genera un punto.

PARABOLOIDE

Caso particular: F(x,y)=0, en R3, representa una superficie con generatriz paralela al eje OZ; esto varía dependiendo de la variable que falte en la función, si falta la variable X sera una superficie con generatriz paralela al eje OX, y lo mismo se aplica para cuando falta la variable Y.

Si F(x,y,z)=0, es una función de primer orden, la ecuación función implícita corresponde al plano.

LA RECTA EN R3.
Las ecuaciones de la recta en el espacio, dado el vector director y un punto que pertenece a la recta son:

Ecuación vectorial de la recta.
Ecuaciones para métricas de la recta

Ecuaciones paramétricas de la recta.
ecuación continua de la recta

Ecuaciones canónicas o cartesianas de la recta.

Segunda Clase.
Seguíamos analizando las ecuaciones de la recta en R3, ahora los datos seran conocidos dos puntos que pertenecen a la recta:

$\overrightarrow{r}=\overrightarrow{r1}+t(\overrightarrow{r2}-\overrightarrow{r1})$ Ecuación vectorial de la recta.

x = x1 +t(x2-x1)

Ecuaciones paramétricas de la recta.
z = z1 +t(z2-z1)

$\frac{x-x1}{x2-x1}=\frac{y-y1}{y2-y1}=\frac{z-z1}{z2-z1}$ Ecuaciones cartesianas, canónicas o simétricas.

DISTANCIA PUNTO-RECTA.

ÁNGULO ENTRE DOS RECTAS.

$\theta=\arccos{(\hat{a1}.\hat{a2})}$ ; donde a1 y a2 son los vectores directores unitarios de las dos rectas.

EL PLANO EN EL ESPACIO.
Las ecuaciones del plano en el espacio dados un punto que pertence al plano y el vector normal, es decir un vector perpendicular al plano, son:

$(\vec{r}-\vec{r0}).\vec{n}=0$ Ecuación vectorial del plano, donde r0 es el vector de posición del punto y n es el vector normal.

eco general del plano

Ecuación general del plano. Donde A, B y C son las componentes del vector normal.

ECUACIONES INCOMPLETAS DEL PLANO.

1. Si C=0.
Ax + By + D = 0, f(x,y)=0 Plano con generatriz paralela al eje OZ.

2. Si C=0 y D=O.
Ax + By = 0, es un plano que pasa por el origen y tiene generatriz paralela al eje OZ y que contiene al eje OZ.

3. Si B=0 y C=0 y D es diferente de 0.
Ax + D = 0. Son planos paralelos al plano YOZ.

ECUACIÓN SEGMENTARIA DEL PLANO.
ecuación canónica de la recta en el espacio

ECUACIÓN NORMAL DEL PLANO.

Conocidos los cosenos directores de un vector perpendicular al plano y siendo d la distancia del plano al origen de coordenadas, la ecuación del plano toma la forma:

Ecuación Normal del Plano

Tercera Clase.

FACTOR NORMALIZANTE. ( $\mu$ )

Para pasar de la ecuación general del plano a la ecuación normal del plano, se multiplica a la ecuación general del plano por un factor normalizante el cual es el siguiente:

$\mu = \pm \frac{1}{\sqrt[]{A^2+B^2+C^2}}$

DISTANCIA DE UN PUNTO A UN PLANO.

Lo que nos indica esa fórmula es que en el numerados se debe remplazar las coordenadas del punto P en la ecuación general del plano al cual queremos sacar la respectiva distancia.

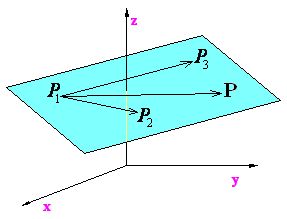
ECUACIÓN DE UN PLANO DADO 3 PUNTOS.
Cuando nos dan 3 puntos hay que escribir los vectores posición de cada uno de los puntos y aplicar la siguiente ecuación:

$(\vec{r}-\vec{r1}).(\vec{r2}-\vec{r1})x(\vec{r3}-\vec{r1})=0$ Ecuación vectorial del plano dado 3 puntos.

Lo cual representa el producto mixto de tres vectores, si el producto mixto de tres vectores es cero, entonces los vectores son cooplanares. Geométricamente el producto mixto de tres vectores representa el volumen del paralelepípedo formado cuyas aristas son los vectores involucrados.

RECTA DETERMINADA POR LA INTERSECCIÓN DE DOS PLANOS.

Para poder encontrar la ecuación de la recta determinada por la intersección de dos planos, se deben conocer las ecuaciones de estos planos, ese sería nuestro dato. Una vez que tengamos las ecuaciones se debe formar un sistema de ecuaciones y dar un valor a una de las variables, para así encontrar las otras dos y obtener un punto que pertenezca a la recta que deseamos encontrar. Una vez obtenido el punto se lo remplaza en la siguiente fórmula y se encuentra la ecuación cartesiana de la recta:

$\frac{x-x0}{\begin{bmatrix}{B1}&{C1}\\{B2}&{C2}\end{bmatrix}}=\frac{y-y0}{\begin{bmatrix}{C1}&{A1}\\{C2}&{A2}\end{bmatrix}}=\frac{z-z0}{\begin{bmatrix}{A1}&{B1}\\{A2}&{B2}\end{bmatrix}}$

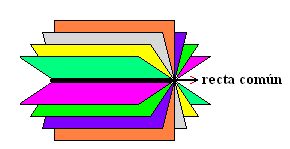
HAZ DE PLANOS.
Conjunto infinito de planos que pasan por una recta común.

ECUACIÓN VECTORIAL DE LA ESFERA.

Ecuación Vectorial de la esfera.

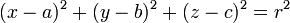(x - a)^2 + (y - b)^2 + (z - c)^2 = r^2\,

Ecuación general o cartesiana de la esfera.

Cuarta Clase.
SUPERFICIES DE SEGUNDO ORDEN.
La ecuación general para cualquier superficie de segundo orden es:
Ax^2+By^2+Cz^2+Exy+Fxz+Hyz+Ix+Ky+Lz+M =0

Ax^2+By^2+Cz^2+Exy+Fxz+Hyz+Ix+Ky+Lz+M =0

Esta ecuación puede simplificarse notablemente si se escoje un sistema de referencia adecuado.
Ejemplos de superficies de segundo orden más comunes:

ELIPSOIDE:

HIPERBOLOIDE DE UNA HOJA:

PARABOLOIDE HIPERBÓLICO:

CILINDROS CUADRÁTICOS:

Quinta Clase.

FUNCIONES VECTORIALES Y CURVAS EN R3.

$F: D\subseteq\mathbb{R}\rightarrow{}\mathbb{R}^ 3$

$t\rightarrow{}$ $\vec{F}(t)=(f1(t);f2(t);f3(t ))$

Cada componente del vector es una función escalar, el dominio de la función es la intersección de los dominios de cada una de las funciones escalares, al igual el rango o recorrido es la unión de todos los rangos de las funciones escalares.

LÍMITES Y CONTINUIDAD.

$\displaystyle\lim_{t \to{t0}}{\vec{F}(t)}=(\displaystyle\lim_{t \to{t0}}{f1(t)},\displaystyle\lim_{t \to{t0}}{f2(t)},\displaystyle\lim_{t \to{t0}}{f3(t )})$

Existirá el límite, si y solo si existen los limites de cada una de las funciones componentes.

Una función es continua en a si cumple que:

$\displaystyle\lim_{t \to{t0}}{\vec{F}(t)}=\vec{F}(a )$

DERIVADAS E INTEGRALES.

$\vec{F }(t)^{\prime}=(f1(t)^{\prime},f2(t)^{\prime},f3(t)^{\prime})$

$\int_a^b\vec{F }(t)dt=(\int_a^bf1(t)dt,\int_a^bf2(t)dt,\int_a^bf3(t)dt)$

Sexta Clase y Séptima Clase.

TRIEDRO MÓVIL

$\vec{T}=\vec{r}(t )^{\prime}$ Vector Tangente

$\vec{B } = \vec{r}^{\prime}\times{}\vec{r}^{\prime\prime}$ Vector Binormal

$\vec{N}=\vec{B}\times{}\vec{ T}$ Vector Normal

$\frac{x-x0 }{Tx}=\frac{y-yo}{Ty}=\frac{z-z0}{Tz}$ Ecuación cartesiana de la Recta Tangente

$\frac{x-x0}{Bx}=\frac{y-yo}{By}=\frac{z -z0}{Bz}$ Ecuación cartesiana de la Recta Binormal

$\frac{x-x0}{Nx}=\frac{y-yo}{Ny}=\frac{z-z0}{N z}$ Ecuación cartesiana de la Recta Normal

Ecuación del Plano Osculador

Ecuación del Plano Rectificante

Ecuación del Plano Normal

$\frac{d\vec{r}}{ds}=\hat{T }$

$\frac{d\hat{T}}{dt}=k\hat{N} \left\|{\frac{d\vec{r }}{dt}}\right\|$ Primera Ecuación de Fernet-Serret

$\frac{d\hat{B }}{dt}=- \tau\hat{N} \left\|{\frac{d\vec{r}}{dt}}\right\|$ Segunda Ecuación de Fernet-Serret

$\frac{d\hat{N}}{dt}=( \tau\hat{B}-k\hat{T}) \left\|{\frac{d\vec{r }}{dt}}\right\|$ Ecuación de Fernet-Serret

Donde: k: es la curvatura de flexión.

$\tau$ : es la curvatura de torsión.

TIPOS DE CURVATURA.

1. CURVATURA DE FLEXIÓN: Se la entiende como la razón de cambio del vector tangente con respecto a la longitud de arco.

$\frac{d\hat{T}}{ds}=K\hat{N }$

$Pk=\frac{1}{k }$ Radio de curvatura

2.CURVATURA DE TORSIÓN: Representa el acercamiento o alejamiento del plano osculador a la curva C; y se la entiende como la variación del ángulo del vector binormal con respecto a la longitud de arco,

$\frac{d\hat{B }}{ds}=- \tau\hat{N}$

$P \tau=\frac{1}{ \tau }$ Radio de curvatura de torsión

Cálculo Vectorial ;)

MENU

OCTUBRE

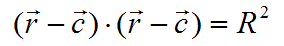
No hay comentarios:

Publicar un comentario